Вот и добрались до одной из важных частей — точек интереса. Т.е. это такие места где может что-то произойти (например, место квеста) или.. просто достопримечательность, куда можно прийти и полюбоваться окружением. И первая точка интереса, практически любой игры, это конечно же лобби или, в нашем случае, это стартовая локация (деревня).
Вот только, для нас, есть одна проблема — у нас генерится холмистая местность и расставлять в ней домики и что либо ещё, несколько.. не удобно. Как следствие, нам нужно сделать горизонтальную поверхность в нашей точке интереса. Это будет некая плоскость, точнее плоская фигура. А какие у нас существуют плоские фигуры? Круг, треугольник, квадрат, ромб, прямоугольник, трапеция, пятиугольник и т.д. и т.п. Исходя из условностей игрового пространства, а так же простоты построения фигур нас могут устроить, те что легко построить и имеют минимум параметров:
- Круг. Задаётся центром и радиусом
- Прямоугольник. Задаётся координатой одной из вершин и длинной каждой из сторон.
- Квадрат. Задаётся центром и половиной длинны стороны или вершиной и длинной стороны.
Почему два варианта нам нужны? Круг — это например, зона где закопан клад или блуждает босс, а прямоугольник — это может быть какое-то строение или подземелье…
Чтобы по параметрам не путать квадрат с кругом, то будем его задавать аналогично прямоугольнику. И выходит что самое простое, это круг. С него и начнём.
Сперва немножко теории. Допустим мы решили задать горизонтальный круг. Значит внутри плоскости круга, у нас будет вертикальная координата постоянной величиной. Это мы можем просто организовать. Если посмотреть сбоку, то будет похожая картина:
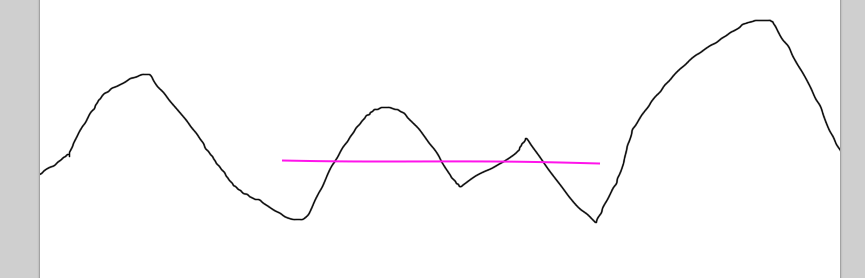
Первый момент. Наша плоскость будет то выше, то ниже сгенерированной местности. Соответственно, на нужно зафиксировать внутреннюю координату Y. Второй момент — резкий переход от сгенерённой поверхности к фиксированному уровню. И вот тут нам помогут знания алгебры и геометрии. Предположим, что у нас не один круг, а два. И получаем три пространства:
- внутреннее — координата Y постоянна
- среднее — координата Y плавно меняется от постоянной на внутреннем радиусе до расчётной на внешнем радиусе
- внешнее — координата Y равна расчётной
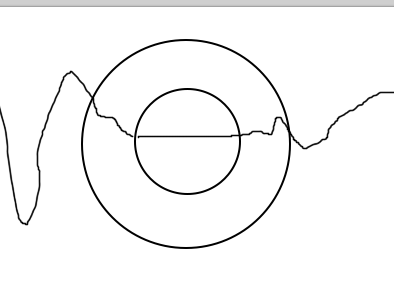
Если чуть-чуть подумать, то чем дальше от внутреннего радиуса, тем больше влияние расчётного относительно базового. Если сделать ещё одно допущение — радиус внешнего равен двум радиусам внутреннего, то всё становится совсем просто:
- У нас есть два радиуса (R1 малый и R2 больший) и у нас есть расстояние R рассчитанной точки отступа от центра
- Если расстояние меньше малого радиуса, то Y равен Y0
- Если расстояние больше большего радиуса, то Y равен расчётному Y1
- Если расстояние лежит между R1 и R2, то тут вступает в силу математика. Y = Y0 + (Y1 — Y0) * ( R — R1) / (R2 — R1) — т.е. возле R1 у нас значение деления будет около нуля (минимальное влияние), а возле R2 значение станет близко 1. Т.е., чем дальше, тем больше влияние рассчитанного значения над базовым.
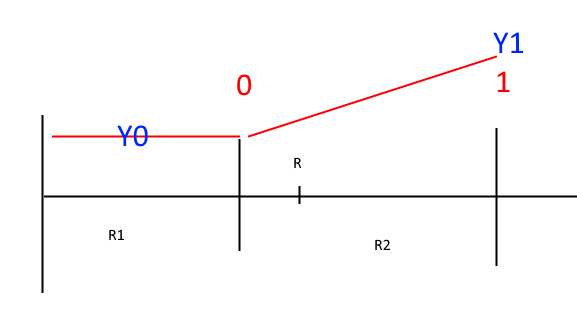
С кругом всё именно так и это довольно легко реализовать. А с прямоугольной областью надо думать, потому что там, как бы, расстояние нужно считать от ближайшей стороны этого прямоугольника, т.е. на которую падает нормаль. Сложно? Потому пока что остановимся на круглой точке интереса и сделаем нашу стартовую зону (мне надоело с неба падать при запуске игры).
В наш конфиг добавим координаты центра деревни: (0, 0, 0) — кто бы сомневался что это будет центр мира. А так же добавим наши радиусы R1 и R2, где R1 неизменный уровень, R2 — ширина перехода. Для примера подойдёт и так:
VillageCenter = Vector3.new(0,0,0), -- координата центра деревни VillageR1 = 100, -- радиус деревни VillageR2 = 200, -- ширина сглаживания
А дальше мы забахаем функцию корректировки нашего расчётного значения Y в TerrainGenerator. Не забываем установить и наш спавнер в координаты (0, 0, 0).
--[[ center - координата центра нормализации position - координата что нужно сгладить R1 - фиксированный радиус для Y R2 - радиус сглаживания Y2 - значение для расчёта Y - возвращаемое значение нормализованного Y ]] function NormalizeY(center: Vector3, position: Vector3, R1, R2) -- warn(center, position) local Y1 = center.Y local Y2 = position.Y local Y = Y1 -- возвращаемое значение local dist = (position - center).Magnitude if dist < R1 then -- ничего не делаем, мы его уже назначили elseif dist > R2 then Y = Y2 else -- а вот тут будем считать Y = Y1 -- базовый уровень + (Y2-Y1) -- разница высот * (dist - R1) -- удаление от R1 / (R2 - R1) -- максимальное удаление end -- warn(dist, Y) return Y end
Мы получили ровную поверхность, которая с удалением начинает холмиться и возвращается к виду как оно было изначально.
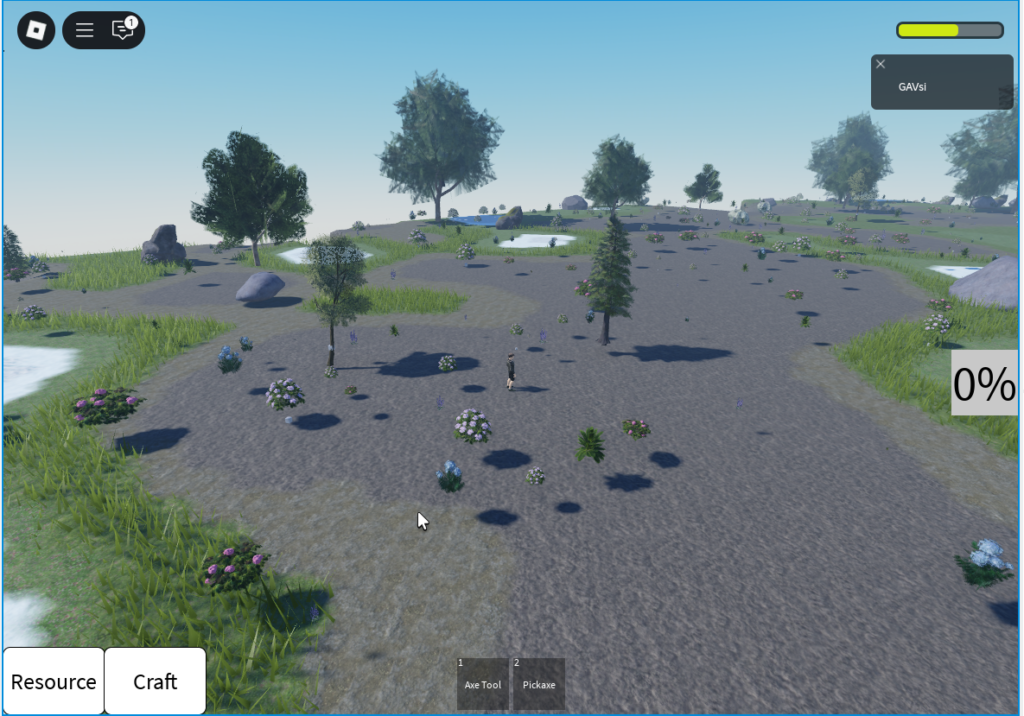
Вот только при очередном запуске у нас всё стало вновь кривое. Как такое получилось? А всё просто — мы берём расстояние по прямой от расчётной точки до центра деревни. А нам нужно только расстояние по плоскости, без учёта координаты Y, ведь её мы и рассчитываем. Добавим создание векторов без учёта вертикали и уже ими будем считать магнитуду.
-- тот самый случай, когда нам НЕ нужны координаты Y local v1 = Vector3.new(center.X, 0, center.Z) local v2 = Vector3.new(position.X, 0, position.Z) local dist = (v1 - v2).Magnitude
Второе что видим это летающие посадки. Тут у нас два выхода — сажать их через рейкаст с неба (правильный вариант), либо просто «углубить» на конкретное число (что и сделаем). Мы ленивые, потому просто опустим их на две трети величины чанка, исправив всего одну строчку.
-- генерация ресурсов CreateResource(x, y - GRID/3*2, z, material)
Ну и радиусы возьмём поменьше. Чтобы и бегать меньше и наглядней было.
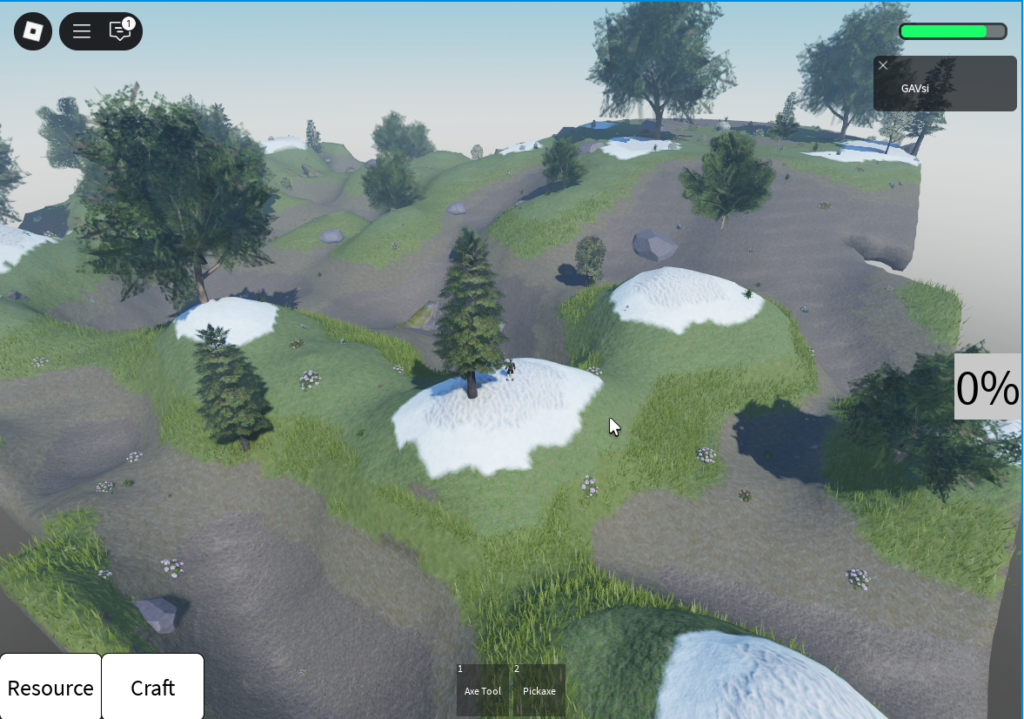
Вроде и стало получше, но что-то не так… С вершин гор практически не видно нашей деревни, да и ямы стали очень глубокими. Выходит где-то у нас ошибка в расчётах. А вот и нет! Дело было не в бобине — раздолбай сидел в кабине! В начале нашего скрипта генерации есть строчка:
local BASE = -HEIGHT -- смещение по вертикали
Вот из-за неё всё и опускалось ниже ватер линии. Ставим туда значение 0 и смотрим на результат:
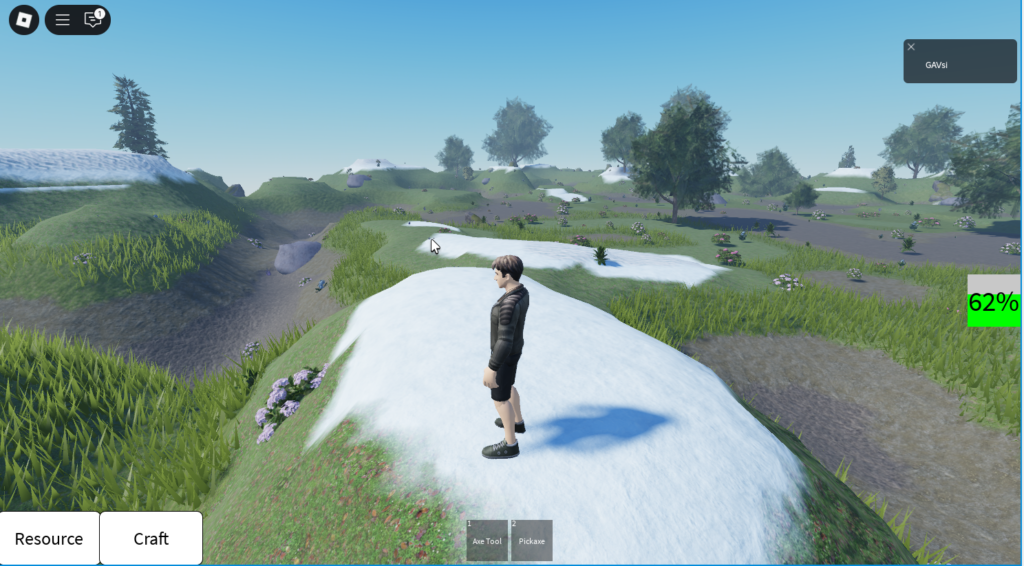
Ну вот, теперь вокруг нашей поляны есть не только ямы, но и холмики. Осталось теперь запретить генерацию ресурсов в пределах деревни и.. что-нибудь в ней разместить. Ну ещё можно задать специальный материал для террейна в её пределах, чтобы уж точно отличать от окружения.
Что же, сперва добавим функцию расчёта дистанции между проекциями векторов на плоскости:
-- дистанция на плоскости между двумя векторами function PlaneDistance(x1: Vector3, x2: Vector3) local v1 = Vector3.new(x1.X, 0, x1.Z ) local v2 = Vector3.new(x2.X, 0, x2.Z) -- разница между векторами в проекции на плоскость return (v1-v2).Magnitude end
А после и добавим условие с заменой материала и запретом генерации ресурса. Вновь меняем нашу функцию генерации чанков:
function CreateChunk(x, z) local y = math.noise(SEED, x/SCALE, z/SCALE) -- получаем координату local material = Enum.Material.Ground if y > 0.5 then material = Enum.Material.Glacier elseif y > 0.4 then material = Enum.Material.Snow elseif y > 0.2 then material = Enum.Material.LeafyGrass elseif y > 0 then material = Enum.Material.Grass elseif y < -0.2 then material = Enum.Material.Mud end y = BASE + HEIGHT * y -- получаем координату -- нормализация с учётом деревни y = NormalizeY(gameConfig.VillageCenter, Vector3.new(x,y,z), gameConfig.VillageR1, gameConfig.VillageR2) local dist = PlaneDistance(gameConfig.VillageCenter, Vector3.new(x,y,z)) local noRes = false -- не генерировать ресурсы if dist < gameConfig.VillageR1 then material = Enum.Material.Asphalt -- в деревне не генерируем ресурсы noRes = true end -- создание ландшафта workspace.Terrain:FillBlock( CFrame.new(x*GRID, y, z*GRID), -- где располагаем Vector3.new(GRID,GRID*2,GRID), -- какого размера material -- что именно ) -- анти фриз (60 кадров в секунду) if workspace:GetServerTimeNow() - timer > 5/60 then timer = workspace:GetServerTimeNow() task.wait() end if noRes == false then -- генерация ресурсов CreateResource(x, y - GRID/3*2, z, material) end end
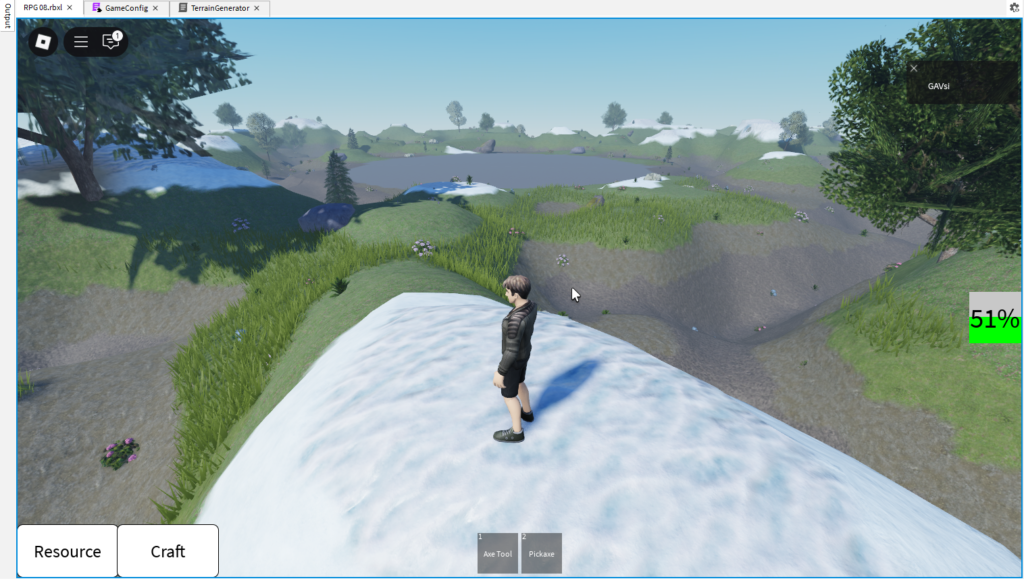
Полученный результат вполне себе ничего. Остаётся в студии построить что-то и посмотреть как это будет выглядеть в режиме игры. Ставлю плиту в 0, якорю и уже на ней ставим декор:

Запускаем и видим совсем не то, что ожидается:
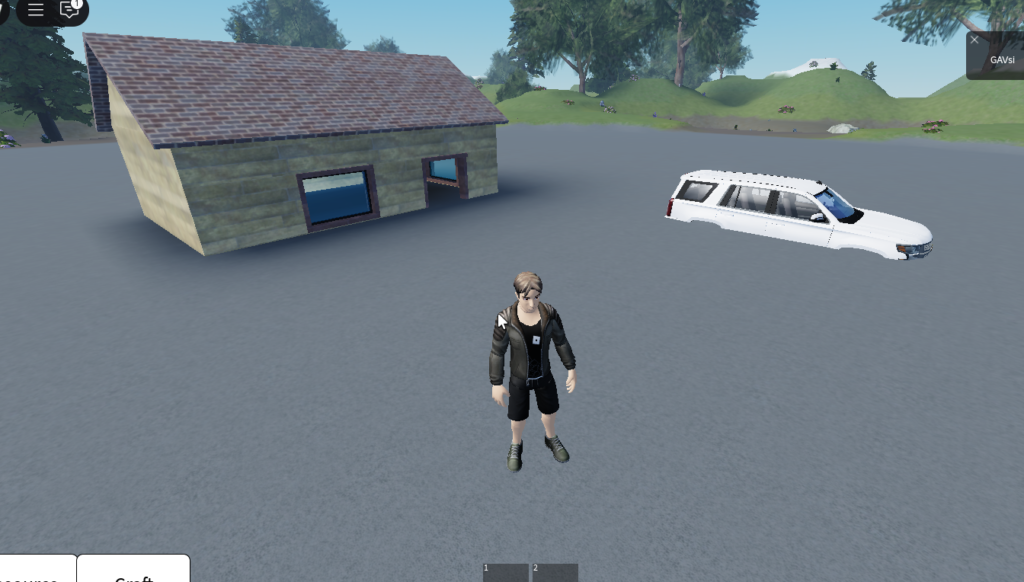
Хотя, в принципе, ожидаемо. Ведь у нас построение чанков идёт от размера сетки, а он у нас равен 4. Отсюда у нас два варианта — поднять всю деревню на размер сетки или же генерацию сместить вниз. Проще, на данном этапе, конечно поднять наши три объекта. Но в будущем нам придётся каждый раз вспоминать про этот момент. И потому мы опустим наш нормализатор. А точнее, нам нужно поставить BASE = -4 и в нормализатор передавать координаты деревни на BASE меньше по Y.
-- нормализация с учётом высоты сетки y = NormalizeY(gameConfig.VillageCenter + Vector3.new(0, BASE, 0), Vector3.new(x,y,z), gameConfig.VillageR1, gameConfig.VillageR2)
Кстати, эта машинка не справилась с нашими горками — ей не хватило мощности и она застряла в яме.

Ну вот, совсем другое дело. Следует добавить что радиус круга вдвое больше по размеру, чем сторона плиты. И… У нас есть ещё SCALE = 15 что увеличивает сглаженность мира. Ну и само собой GRID = 4 , что задаёт базовый размер ячейки. Если SCALE мы можем игнорировать, то остальное значит что, чтобы постамент под деревней был нужного размера, то он должен быть в 2*4 раз большего размера, чтобы в него полностью вписался круг деревни. Либо, если нам нужно наоборот, вписать квадрат в круг, то длинна его стороны должна быть — диагональ круга разделить на корень квадратный из двух:

Что же касаемо прямоугольников, то тут всё сложно. Чтобы корректно сглаживать, нам нужно точно рассчитать длину нормали к ближайшей точке на стороне прямоугольника или его вершины.
В принципе, нам может помочь одно допущение — стороны прямоугольника должны быть заданы параллельными осям координат. И тогда мы мы сможем просто проверить находится ли точка внутри одного из прямоугольников или за их пределами.
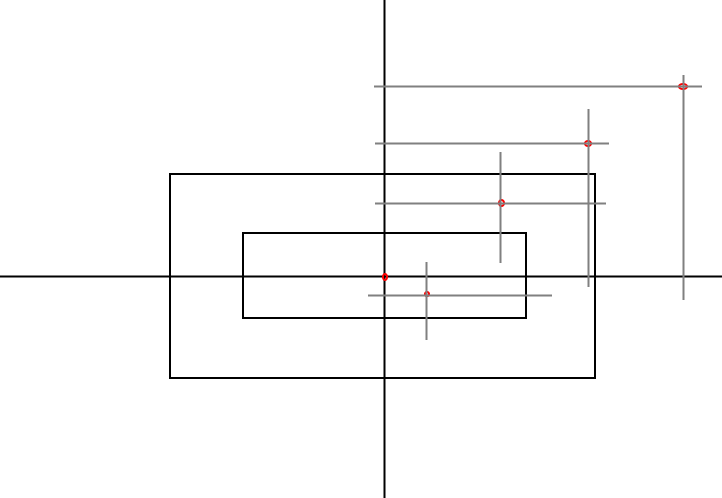
После нашего допущения мы видим, что у нас осталось всего четыре варианта размещения точек:
- внутри меньшего прямоугольника — он задаём саму площадь объекта
- внутри большего прямоугольника — он задаёт территорию сглаживания
- за пределами большего прямоугольника, но в пределах его стороны
- полностью за пределами большего прямоугольника
В принципе, два последних можно бы и объединить, там расчёт будет стандартный. Вариант внутри меньшего — это значит у нас высота Y будет константой. А вот внутри большего и вне меньшего — это как раз наш вариант сглаживания и с учётом нашего допущения (что стороны параллельны осям) рассчитать удаление становится очень просто — нужно просто вычислить минимальное расстояние из всех координат сторон меньшего прямоугольника (ну вообще-то по соответствующей координате их будет две пары).
Остаётся только определиться как мы будем задавать наши прямоугольники?
- по координатам двух диагональных углов
- по одной из вершин и длин его сторон
- по координатам центра и длин его сторон
Если исходить из того, как мы задавали круг, то и тут нам нужен центр и длинны сторон. Вторая причина — когда будем распределять по пространству, нам нужно будет совмещать разные зоны между собой. А что будет если зоны выравнивания будут пересекаться? Ничего особенного, они будут многократно сглаживаться (от количества пересечений). И зная это нам нужно будет иметь это ввиду расставляя зоны интереса на карте. Т.е. они либо не должны пересекаться, либо должны находиться на одной высоте. Далеко не с первого раза получилась вот такая функция нормализации прямоугольной зоны интереса.
--[[ Нормализация вертикальной координаты относительно прямоугольника center - координата центра нормализации position - координата что нужно сгладить X1 - длинна стороны X X2 - длинна сглаживания по стороне X >X1 Z1 - длинна стороны Z Z2 - длинна сглаживания по стороне Z >Z1 Y - возвращаемое значение нормализованного Y ]] function NormalizeSquareY(center: Vector3, position: Vector3, X1, X2, Z1, Z2) local Y1 = center.Y local Y2 = position.Y local Y = Y1 -- возвращаемое значение local pos = 0 -- 0 не рассчитано, 1 - внутри малого зоны, 2 - внутри прямоугольника сглаживания, 3 вне регулирования local dist = math.huge -- дистанция удаления if position.X > center.X - X1/2 and position.X < center.X + X1/2 then -- могут быть все варианты -- внутри малого периметра Х if position.Z > center.Z - Z1/2 and position.Z < center.Z + Z1/2 then -- внутри малого прямоугольника Y = Y1 elseif position.Z > center.Z - Z2/2 and position.Z < center.Z + Z2/2 then -- внутри большого по координате Z if position.Z < center.Z then dist = (center.Z - Z1/2) - position.Z -- расстояние от границы else dist = position.Z - (center.Z + Z1/2) -- расстояние от границы end local k = dist / (Z2/2 - Z1/2) -- коэффициент сглаживания local deltaY = k * (Y2 - Y1) -- на сколько изменится разница высот Y = Y1 + deltaY -- итоговое значение высоты else -- вне зоны сглаживания Y = Y2 end elseif position.X > center.X - X2/2 and position.X < center.X + X2/2 then -- могут быть варианты 2 и 3 -- внутри большого периметра Х (даже если в малый попадают, то они уже за пределами по другой координате) if position.Z > center.Z - Z1/2 and position.Z < center.Z + Z1/2 then -- нужно проверить только одно удаление if position.X < center.X then dist = (center.X - X1/2) - position.X else dist = position.X - (center.X + X1/2) end local k = dist / (X2/2 - X1/2) -- коэффициент сглаживания local deltaY = k * (Y2 - Y1) -- на сколько изменится разница высот Y = Y1 + deltaY -- итоговое значение высоты elseif position.Z > center.Z - Z2/2 and position.Z < center.Z + Z2/2 then -- нужно проверить оба удаления if position.X < center.X then dist = (center.X - X1/2) - position.X else dist = position.X - (center.X + X1/2) end local k1 = dist / (X2/2 - X1/2) -- коэффициент сглаживания if position.Z < center.Z then dist = (center.Z - Z1/2) - position.Z -- расстояние от границы else dist = position.Z - (center.Z + Z1/2) -- расстояние от границы end local k2 = dist / (Z2/2 - Z1/2) -- коэффициент сглаживания local k = math.max(k1, k2) -- берём максимальное значение local deltaY = k * (Y2 - Y1) -- на сколько изменится разница высот Y = Y1 + deltaY -- итоговое значение высоты else Y = Y2 end else -- за пределами регулирования Y = Y2 end return Y end
Правда я подумал и добавил табличку с перечнем прямоугольных зон, ведь их у нас может быть мульён.
return {
{ -- пример прямоугольной зоны интереса
Vector3.new(50, 0, 50), -- центр зоны
20, -- длинна X стороны -- от центра это только половина значения
40, -- граница сглаживания по X
40, -- длинна Z стороны
80, -- граница сглаживания по Z
Enum.Material.Sandstone -- материал поверхности - не обязательный параметр
}
}
Саму деревню пока что не будем переделывать под прямоугольник… Ну а результат, напряга нашего мозга, вполне не плох:

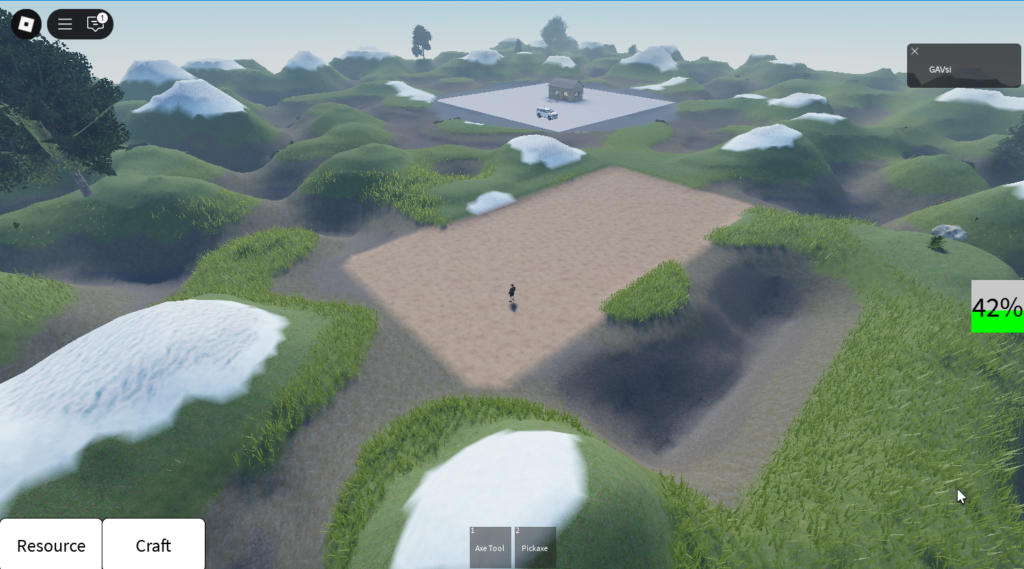
А имея возможность построения зоны интереса и зная её размеры — можно горы чего наворотить.
Попробуем уменьшить, но сделать их несколько рядом. Зададим табличку вот такого формата:
return {
{ -- пример прямоугольной зоны интереса
Vector3.new(30, 0, 30), -- центр зоны
20, -- длинна X стороны -- от центра это только половина значения
40, -- граница сглаживания по X
30, -- длинна Z стороны
50, -- граница сглаживания по Z
Enum.Material.Sandstone -- материал поверхности - не обязательный параметр
},
{ -- пример прямоугольной зоны интереса
Vector3.new(30, 0, 60), -- центр зоны
20, -- длинна X стороны -- от центра это только половина значения
40, -- граница сглаживания по X
30, -- длинна Z стороны
50, -- граница сглаживания по Z
Enum.Material.Salt -- материал поверхности - не обязательный параметр
},
{ -- пример прямоугольной зоны интереса
Vector3.new(60, 0, 60), -- центр зоны
20, -- длинна X стороны -- от центра это только половина значения
40, -- граница сглаживания по X
30, -- длинна Z стороны
50, -- граница сглаживания по Z
Enum.Material.Asphalt -- материал поверхности - не обязательный параметр
},
{ -- пример прямоугольной зоны интереса
Vector3.new(60, 0, 30), -- центр зоны
20, -- длинна X стороны -- от центра это только половина значения
40, -- граница сглаживания по X
30, -- длинна Z стороны
50, -- граница сглаживания по Z
Enum.Material.Concrete -- материал поверхности - не обязательный параметр
},
}
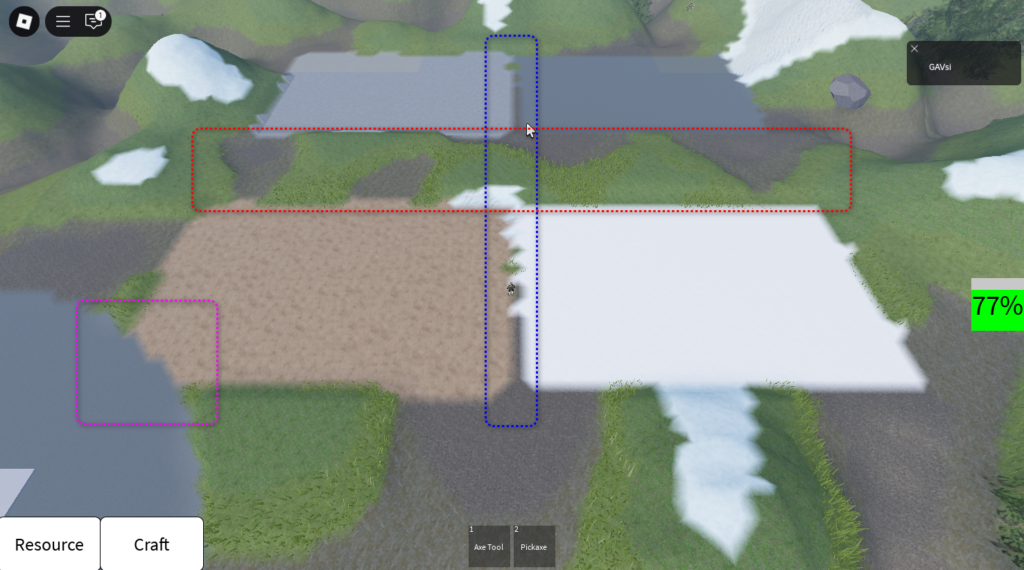
Как видим, где они у нас на уровне и касаются (синий), там ровный уровень. Где между ними есть относительное расстояние(красный), там уже есть неровности сглаживания. Ну и деревня перекрывает наш прямоугольник, т.к. она последняя в коде.
В принципе, на этом мысль о точках интереса и закончим. Как их организовать разобрали, а вот чем наполнять это отдельная песня.
По традиции, обновлённый плейс: